Potentialströmung: Unterschied zwischen den Versionen

Die Strömung eines Fluids (Flüssigkeit oder Gas) ist eine Potentialströmung, wenn das Vektorfeld der Geschwindigkeiten mathematisch so geartet ist, dass es ein Potential besitzt. Das Potential kann man sich anschaulich als die Höhe in einer Reliefkarte vorstellen, wo dann die Richtung der größten Steigung in einem Punkt der dortigen Geschwindigkeit entspricht. Ein solches Potential ist in einem homogenen Fluid vorhanden, wenn die Strömung rotationsfrei (wirbel- bzw. vortizitätsfrei) ist und keine Zähigkeitskräfte (Reibungskräfte) auftreten oder diese vernachlässigbar klein sind. Jede aus der Ruhe heraus beginnende Strömung eines homogenen, viskositätsfreien Fluids besitzt ein solches Potential.^[1]

Eine Potentialströmung ist der rotationsfreie Spezialfall der Strömung eines homogenen, viskositätsfreien Fluids, das durch die Euler’schen Gleichungen beschrieben wird; diese gelten auch für Strömungen mit Rotation (Wirbelströmung). Wenn jedoch bei Scherbewegungen die Zähigkeit berücksichtigt werden muss, wie z. B. in Grenzschichten oder im Zentrum eines Wirbels, so ist mit den Navier-Stokes-Gleichungen zu rechnen.

Potentialströmungen können als sehr gute Näherung von laminaren Strömungen bei niedrigen Reynolds-Zahlen verwendet werden, wenn die fluiddynamische Grenzschicht an den Rändern der Strömung keine wesentliche Rolle spielt. In der stationären Potentialströmung inkompressibler Fluide gilt die bernoullische Druckgleichung global, die technische Rohrströmungen gut beschreibt. Wegen ihrer einfachen Berechenbarkeit werden Potentialströmungen auch als Anfangsnäherung bei der iterativen Berechnung der Navier-Stokes-Gleichungen in der numerischen Strömungsmechanik verwendet.

Definition

Eine Potentialströmung ist eine Strömung, die ein Geschwindigkeitsfeld $ {\vec {v}}({\vec {x}},t) $ besitzt, das vom Ort $ {\vec {x}} $ und von der Zeit t abhängt und sich aus dem Gradient „grad“ eines Geschwindigkeitspotentials $ \phi ({\vec {x}},t) $ berechnet:

$ {\vec {v}}=\operatorname {grad} (\phi )\quad \Leftrightarrow \quad v_{i}={\frac {\partial \phi }{\partial x_{i}}}\,,\;i=1,2,3 $

Deshalb werden solche Strömungen Potentialströmungen genannt. Die linke Vektorgleichung ist die koordinatenfreie Version, während die rechten Gleichungen in kartesischen Koordinaten $ x_{1,2,3} $ gelten.

Jedes Gradientenfeld ist rotationsfrei, weshalb Potentialströmungen immer rotationsfrei sind. Umgekehrt existiert nach dem Poincaré-Lemma immer dann ein Geschwindigkeitspotential, wenn die Strömung rotationsfrei ist.

Anwendungsbereiche und Limitierungen

Potentialströmungen enthalten nicht alle Charakteristika von realen Strömungen. Die inkompressible Potentialströmung macht eine Reihe von falschen Voraussagen, wie beispielsweise das d’Alembert’sche Paradoxon, demgemäß von der Strömung auf einen Körper keine Kraft in Richtung der Strömung ausgeübt wird. Alle Phänomene, die eine hydrodynamische Grenzschicht oder turbulente Strömung nebst Dissipation von Energie beinhalten, wie z. B. Strömungsabrisse, können mit Potentialströmungen nicht abgebildet werden.

Nichtsdestotrotz ist das Verständnis von Potentialströmungen in vielen Bereichen der Strömungsmechanik hilfreich. So können für nicht zu komplizierte Geometrien analytische Lösungen ihrer Umströmung berechnet werden und auch die von der Strömung geleistete Auftriebskraft angegeben werden. So wird ein tieferes Verständnis der Strömung erreicht.

Potentialströmungen finden viele Anwendungen in der Auslegung von Flugzeugen. Wie eingangs erwähnt können Potentialströmungen als sehr gute Näherung von laminaren Strömungen bei niedrigen Reynolds-Zahlen verwendet werden, wenn die hydrodynamische Grenzschicht an den Rändern der Strömung keine wesentliche Rolle spielt. Eine Technik in der numerischen Strömungsmechanik koppelt eine viskose Grenzschichtströmung an eine Potentialströmung außerhalb der Grenzschicht. In einer Potentialströmung kann jede Stromlinie durch eine Wand ersetzt werden, ohne die Strömung dadurch zu verändern, eine Technik, die im Flugzeugdesign angewendet wird.

Bestimmungsgleichungen für die Strömung

Nicht jedes Geschwindigkeitspotential repräsentiert eine physikalisch plausible Strömung. Damit das Geschwindigkeitspotential unter den getroffenen Annahmen im Einklang mit den physikalischen Gesetzen ist, muss es der Bilanzgleichung für den Impuls in Form der Euler’schen Gleichungen gehorchen und die Massenbilanz erfüllen.

Bilanzgleichungen

Die Impulsbilanz in Form der Euler’schen Gleichungen lautet

$ {\frac {\partial {\vec {v}}}{\partial t}}+\operatorname {grad} ({\vec {v}})\cdot {\vec {v}}+{\frac {1}{\rho }}\operatorname {grad} (p)={\vec {k}} $

und die Massenbilanz

$ {\dot {\rho }}+\rho \operatorname {div} ({\vec {v}})=0 $

Darin ist ρ die Dichte und der aufgesetzte Punkt die substantielle Zeitableitung, „div“ die Divergenz eines Vektorfeldes, p der Druck und $ {\vec {k}} $ ein Beschleunigungsfeld (z. B. Schwerebeschleunigung). Dieses System aus vier Gleichungen mit fünf Unbekannten (drei Geschwindigkeiten, Druck und Dichte) wird durch eine Zustandsgleichung geschlossen, die die Dichte als Funktion des Drucks darstellt.

Einsetzen des Potentials in die Euler’schen Gleichungen liefert mit der Graßmann-Entwicklung^[2]:

$ {\begin{aligned}{\frac {\partial {\vec {v}}}{\partial t}}+\operatorname {grad} ({\vec {v}})\cdot {\vec {v}}+{\frac {1}{\rho }}\operatorname {grad} (p)=&\\{\frac {\partial {\vec {v}}}{\partial t}}+{\frac {1}{2}}\operatorname {grad} ({\vec {v}}\cdot {\vec {v}})-{\vec {v}}\times \operatorname {rot} ({\vec {v}})+{\frac {1}{\rho }}\operatorname {grad} (p)=&\\\operatorname {grad} \left({\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\operatorname {grad} (\phi )^{2}\right)+{\frac {1}{\rho }}\operatorname {grad} (p)=&{\vec {k}}\end{aligned}} $

weil die Rotation eines Gradientenfeldes verschwindet. Die Massenbilanz formt sich mit dem Geschwindigkeitspotential und dem Laplace-Operator $ \Delta =\operatorname {div\circ grad} $ um zu:

$ {\dot {\rho }}+\rho \operatorname {div(grad} (\phi ))={\dot {\rho }}+\rho \Delta \phi =0 $

Nun handelt es sich um ein System aus vier Gleichungen mit drei Unbekannten (Potential, Druck und Dichte), das nur lösbar ist, wenn die Differenz $ {\vec {f}}:={\vec {k}}-{\tfrac {1}{\rho }}\operatorname {grad} (p) $ die Integrabilitätsbedingung $ \operatorname {rot} ({\vec {f}})={\vec {0}} $ erfüllt. Dies ist in barotropen Fluiden in einem konservativen Schwerefeld der Fall.

Barotropes Fluid in konservativem Schwerefeld

In einem barotropen Fluid ist die Dichte nur eine Funktion des Drucks. Dann kann die Integration der Euler-Gleichungen vorab erfolgen, was die Berechnung wesentlich vereinfacht. Barotrope Strömungen liegen dann vor, wenn das Temperaturfeld homogen ist oder wenn im technisch besonders wichtigen Fall die Strömung homentrop ist.^[3]

In einem barotropen Fluid gibt es eine Druckfunktion P mit der Eigenschaft

$ P:=\int {\frac {\mathrm {d} p}{\rho (p)}}\quad \Leftrightarrow \quad \mathrm {d} P={\frac {\mathrm {d} p}{\rho }}\quad \Leftrightarrow \quad \operatorname {grad} P={\frac {1}{\rho }}\operatorname {grad} p $

In einem inkompressiblen Fluid ist die Dichte konstant und P = p/ρ. Einsetzen der Druckfunktion in die Euler-Gleichung erlaubt es, den Gradientenoperator heraus zu ziehen:

$ \operatorname {grad} \left({\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\operatorname {grad} (\phi )^{2}\right)+{\frac {1}{\rho }}\operatorname {grad} (p)=\operatorname {grad} \left({\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\operatorname {grad} (\phi )^{2}+P\right)={\vec {k}} $

Damit diese Gleichung erfüllt werden kann, muss das Beschleunigungsfeld $ {\vec {k}} $ der Integrabilitätsbedingung $ \operatorname {rot} {\vec {k}}={\vec {0}} $ entsprechen. Dann gibt es nach dem Poincaré-Lemma ein Potential V mit der Eigenschaft $ {\vec {k}}=-\operatorname {grad} V $ und die obige Gleichung führt auf ein Gradientenfeld

$ \operatorname {grad} \left({\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\operatorname {grad} (\phi )^{2}+P+V\right)={\vec {0}} $

das überall verschwindet, weshalb der Term in den großen Klammern ortsunabhängig ist:

$ {\frac {\partial \phi }{\partial t}}+{\frac {1}{2}}\operatorname {grad} (\phi )^{2}+P+V=C $

Die Integrationskonstante C könnte noch von der Zeit abhängen aber diese Zeitabhängigkeit kann dem Potential $ \phi $ zugeschlagen werden, ohne dass sich dessen physikalische Bedeutung $ \operatorname {grad} (\phi )={\vec {v}} $ ändern würde^[4].

Nun handelt es sich um ein geschlossenes System aus drei Gleichungen (inklusive ρ=ρ(p) und der Massenbilanz) mit drei Unbekannten Potential, Dichte und Druck.

Stationäre Strömung

In einer stationären Potentialströmung ohne Beschleunigungsfeld gilt^[5]:

$ {\begin{aligned}&\left(1-M_{x}^{2}\right){\frac {\partial ^{2}\phi }{\partial x^{2}}}+\left(1-M_{y}^{2}\right){\frac {\partial ^{2}\phi }{\partial y^{2}}}+\left(1-M_{z}^{2}\right){\frac {\partial ^{2}\phi }{\partial z^{2}}}\\&-2M_{x}M_{y}{\frac {\partial ^{2}\phi }{\partial x\,\partial y}}-2M_{y}M_{z}{\frac {\partial ^{2}\phi }{\partial y\,\partial z}}-2M_{z}M_{x}{\frac {\partial ^{2}\phi }{\partial z\,\partial x}}=0\end{aligned}} $

mit den Machzahlen

$ M_{x}={\frac {1}{c}}{\frac {\partial \phi }{\partial x}},\qquad M_{y}={\frac {1}{c}}{\frac {\partial \phi }{\partial y}},\qquad {\text{und}}\qquad M_{z}={\frac {1}{c}}{\frac {\partial \phi }{\partial z}}, $

und der lokalen Schallgeschwindigkeit c. Die Strömungsgeschwindigkeit $ {\vec {v}}=\operatorname {grad} (\phi ) $ ergibt sich aus dem Gradient des Geschwindigkeitspotentials. Diese Gleichungen sind bei sub-, trans- und supersonischer Strömung anwendbar, so lange ihre Rotationsfreiheit gegeben ist.^[5]

Im sub- oder supersonischen Bereich (aber nicht im transsonischen) kann bei kleinen Anströmwinkeln von schlanken Körpern eine weitere Annahme getroffen werden: Das Geschwindigkeitspotential wird in eine Parallelströmung $ v_{\infty }x $ und ein kleines Störungsfeld $ \varphi $ aufgeteilt: $ \phi =v_{\infty }x+\varphi $. In diesem Fall kann die linearisierte Potentialgleichung – eine Näherung der kompletten Gleichung – benutzt werden^[5]:

$ (1-M_{x}^{2}){\frac {\partial ^{2}\varphi }{\partial x^{2}}}+{\frac {\partial ^{2}\varphi }{\partial y^{2}}}+{\frac {\partial ^{2}\varphi }{\partial z^{2}}}=0 $

Schallwellen

Schallwellen mit geringer Amplitude können mit dem folgenden Potentialströmungsmodell approximiert werden^[6]:

$ {\frac {\partial ^{2}\phi }{\partial t^{2}}}={\bar {c}}^{2}\Delta \phi $

Darin ist $ {\bar {c}} $ die mittlere Schallgeschwindigkeit im homogenen Fluid. Diese Gleichung ist eine Wellengleichung, die für das Geschwindigkeitspotential Φ und gleichfalls für den Druck sowie die Dichte gilt.

Randbedingungen

Die Dirichlet-Randbedingungen geben den Wert des Geschwindigkeitspotentials auf einer Fläche vor, woraus sich die Tangentialgeschwindigkeit des Fluids auf der Fläche ergibt. Mit Neumann-Randbedingungen werden die Ableitungen des Potentials senkrecht zu Flächen festgelegt, was hier der Vorgabe von Geschwindigkeitskomponenten senkrecht zur Fläche entspricht. Ansonsten gilt das bei den Euler’schen Gleichungen zu den Randbedingungen gesagte.

Zirkulation

In einem stationären Strömungsgebiet, in dem die Bernoulli-Gleichung auf allen Stromlinien denselben Wert hat, ist die Zirkulation im inneren des Gebiets gleich Null und die Strömung eine Potentialströmung. Trotzdem können bei einer aus der Ruhe heraus entstehenden Bewegung einer homogenen reibungslosen Flüssigkeit Wirbel entstehen. Denn alle im Ruhezustand im Innern der Flüssigkeit gezogenen (materiellen) Linien weichen bei einsetzender Strömung einer sich bildenden Trennfläche aus und schneiden diese niemals. Der Kelvin’sche Wirbelsatz bezieht sich auf materielle Linien und sagt demnach über die Beziehungen der Gebiete auf beiden Seiten der Trennfläche nichts aus. Deshalb können aus der Ruhe heraus an Kanten Trennflächen und Wirbel ohne Widerspruch zum Wirbelstatz entstehen.^[7]

Da auch der #Potentialwirbel eine Potentialströmung ist, eine von null verschiedene Zirkulation aufweist und inkompressible Potentialströmungen superponierbar sind, kann mit einem Potentialwirbel in oder außerhalb des Strömungsgebietes eine Zirkulation eingebracht werden. Allgemeiner kann ein divergenzfreier Geschwindigkeitsanteil superponiert werden, der sich aus der Rotation eines Vektorfeldes ergibt, dessen Berechnung die Kenntnis der Rotationsverteilung erfordert und die Lösung zusätzlich erschwert.^[8]

Potentialströmung eines inkompressiblen Fluids

Die Annahme der Inkompressibilität ist für Flüssigkeiten bei moderaten Drücken und für Gasströmungen weit unterhalb der Schallgeschwindigkeit eine häufig sinnvolle Näherung. In diesem Fall entkoppeln sich die Bestimmungsgleichungen für die Geschwindigkeit und den Druck: Aus der Laplace-Gleichung bestimmt sich mit den Randbedingungen das Potential und aus den Euler-Gleichungen, die sich auf die Bernoulli’sche Druckgleichung reduzieren, der Druck.

Bestimmungsgleichungen

Bei Inkompressibilität ist das Geschwindigkeitsfeld divergenzfrei

$ \operatorname {div} {\vec {v}}=\operatorname {div(grad} (\phi ))=\Delta \phi =0 $

weswegen das Potential die Laplace-Gleichung erfüllt. Auf Grund der Massenbilanz $ {\dot {\rho }}+\rho \Delta \phi ={\dot {\rho }}=0 $ ist die Dichte zumindest zeitlich konstant; bei Inkompressibilität ist sie auch räumlich konstant. Bei konstanter Dichte vereinfacht sich die bei den barotropen Fluiden eingeführte Druckfunktion P zu P=p/ρ. Multiplikation der Euler-Gleichungen mit der Dichte liefert dann:

$ \rho {\frac {\partial \phi }{\partial t}}+{\frac {\rho }{2}}\operatorname {grad} (\phi )^{2}+p+\rho V=E $

In einer stationären Strömung entfällt der erste Term und es verbleibt die Bernoulli’sche Druckgleichung, die hier im gesamten Strömungsgebiet gilt. Die Konstante Energie E ist die Summe aus kinetischer, innerer (Druck p) und äußerer Energie (Schwerefeld ρV) eines Fluidpartikels und diese Gesamtenergie ist für alle Partikel in der stationären Strömung gleich.

Analogon der Wärmeleitung

Vergleich der über Wärmeleitung berechneten Strömung (farbig und schwarz) mit den analytischen Stromlinien (weiß)

Das Betragsquadrat des Wärmestromes entspricht der Druckverteilung

Eine Potentialströmung kann mit Finite-Elemente-Programmen berechnet werden, in denen die Wärmeleitungsgleichung implementiert ist, was in vielen gängigen Programmen der Fall ist. Die stationäre Wärmeleitung in einem homogenen Festkörper ohne innere Wärmequellen gehorcht der Laplace-Gleichung

$ \Delta T=0 $

weshalb die Temperatur T dort derselben Bestimmungsgleichung unterliegt wie das Geschwindigkeitspotential Φ in einem inkompressiblen Fluid. Wird die Temperatur in einem Festkörper als Geschwindigkeitspotential aufgefasst, dann entspricht der Temperaturgradient, zu dem der Wärmestrom proportional ist, der Strömungsgeschwindigkeit. Die Dirichlet-Randbedingungen legen die Temperaturen auf Oberflächen fest, wodurch sich der Temperaturgradient und mithin die tangentiale Strömungsgeschwindigkeit in der Fläche vorgeben lässt. Neumann-Randbedingungen bestimmen die Wärmestromdichte, die in der Potentialströmung die Normalgeschwindigkeit zur Wand einstellt.

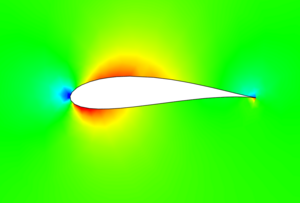
Das obere Bild zeigt einen Ausschnitt der Temperaturverteilung aus einer Wärmeleitungsrechnung mit der Finite-Elemente-Methode in einer quadratischen Scheibe mit einem mittig ausgesparten Profil, das im Beispiel unten behandelt wird. Die Temperatur ist farbkodiert von rot nach blau (rot hoch, blau gering) gezeichnet und die von oben nach unten verlaufenden schwarzen Linien sind ihre Höhenlinien. Die von links nach rechts orientierten kurzen, schwarzen Striche stellen Wärmeströme dar. Um Randeffekte gering zu halten, ist die Scheibe zehnmal so groß wie das Profil, denn die im Beispiel unten, analytisch berechneten, weiß gezeichneten Stromlinien gelten für eine Strömung in der gesamten, wandfreien Ebene. An den Grenzen der Scheibe (außerhalb des Bildes) oben und unten sowie am Profil wurden keine Randbedingungen definiert. Am linken Rand wurde die Wärmestromdichte von eins vorgegeben und am rechten Rand die Wärmestromdichte von minus eins sowie mittig die Temperatur null festgelegt. Mit einer konstanten Temperatur an der rechten Begrenzung wäre ein senkrechter Ausfluss bestimmt worden. Die Höhenlinien der Temperatur entsprechen den Höhenlinien des Geschwindigkeitspotentials und sind im Einklang mit der Theorie augenscheinlich senkrecht zu den weißen Stromlinien und die Wärmeströme sind mit den Stromlinien verträglich.

Das untere Bild zeigt das Betragsquadrat des Wärmestromes (rot groß, blau klein), von dem nach der Bernoulli-Gleichung ohne Schwerebeschleunigung

$ p=E-{\frac {\rho }{2}}\operatorname {grad} (\phi )^{2} $

der Druck eine lineare Funktion ist. Wegen des negativen Vorzeichens herrscht also in den blauen Bereichen ein hoher Druck und in den roten ein niedriger.

Ebene Potentialströmung

Wenn die Strömung in der Ebene stattfindet, dann können die Eigenschaften komplexer Funktionen ausgenutzt werden. Es wird ein komplexes Geschwindigkeitspotential definiert, dessen Realteil das reelle Geschwindigkeitspotential und dessen Imaginärteil die Stromfunktion ist. Beide Funktionen beschreiben dieselbe Strömung. Deshalb gelten die aus der Stromfunktion abgeleiteten Aussagen: Die Höhenlinien der Stromfunktion sind Stromlinien, zwischen denen der Volumenstrom überall gleich ist. Komplexe Geschwindigkeitspotentiale können aus einfacheren zusammengesetzt und transformiert werden, so dass mit einfachen Mitteln komplizierte Strömungen untersucht werden können. Insbesondere kann auch die von der Strömung auf den Körper ausgeübte Kraft exakt berechnet werden.

Komplexes Geschwindigkeitspotential

Die Ebene wird als komplexe Zahlenebene aufgefasst, in der der Wert des Potentials als Realteil einer holomorphen Funktion f dargestellt wird:

$ f(z)=\phi (x,y)+\mathrm {i} \,\psi (x,y)\quad {\text{mit}}\quad z=x+\mathrm {i} \,y\in \mathbb {C} $

Die Menge $ \mathbb {C} $ enthält alle komplexen Zahlen und i ist die imaginäre Einheit. Die Funktion f ist das komplexe Geschwindigkeitspotential, aus dem sich die Geschwindigkeit über die Ableitungen

$ v_{x}={\frac {\partial \phi }{\partial x}}\;,\quad v_{y}={\frac {\partial \phi }{\partial y}}\quad {\text{oder}}\quad w:=v_{x}-\mathrm {i} \,v_{y}={\frac {\mathrm {d} f}{\mathrm {d} z}} $

ergibt. Hier ist w die komplexe Geschwindigkeit. Der Imaginärteil des Potentials ist die Stromfunktion, deren Höhenlinien Stromlinien sind. Weil die Funktion f holomorph ist, gelten die Cauchy-Riemann’schen Differentialgleichungen

$ {\frac {\partial \phi }{\partial x}}={\frac {\partial \psi }{\partial y}}\quad {\text{und}}\quad {\frac {\partial \phi }{\partial y}}=-{\frac {\partial \psi }{\partial x}} $

weswegen die Gradienten des reellen Geschwindigkeitspotentials und der Stromfunktion zueinander senkrecht sind:

$ \operatorname {grad} (\phi )\cdot \operatorname {grad} (\psi )=0 $

Die Gradienten sind wiederum orthogonal zu den Höhenlinien, so dass auch diese sich im rechten Winkel schneiden. Weitere Differentiation offenbart

$ {\begin{aligned}{\frac {\partial ^{2}\phi }{\partial x^{2}}}&={\frac {\partial ^{2}\psi }{\partial y\partial x}}=-{\frac {\partial ^{2}\phi }{\partial y^{2}}}\quad \Rightarrow \quad \Delta \phi =0\\{\frac {\partial ^{2}\psi }{\partial y^{2}}}&={\frac {\partial ^{2}\phi }{\partial x\partial y}}=-{\frac {\partial ^{2}\psi }{\partial x^{2}}}\quad \Rightarrow \quad \Delta \psi =0\end{aligned}} $

weswegen sowohl der real- als auch der imaginäre Teil des komplexen Geschwindigkeitspotentials die Laplace-Gleichung in der Ebene erfüllt. Die obere Gleichung legt die Divergenzfreiheit und die untere die Rotationsfreiheit der Strömung fest.

Aus den Randbedingungen berechnet sich das Potential, aus dem sich über die Ableitungen das Geschwindigkeitsfeld berechnet, und der Druck wird aus der Bernoulli’schen-Druckgleichung ermittelt.

Näherungsweise rechnerische Lösung

Der Laplace-Operator hat in der Ebene in einem regelmäßigen Netz mit Maschenweite $ \triangle x=\triangle y=h $ den Differenzenquotient

$ {\begin{aligned}\Delta \psi =&{\frac {\triangle ^{2}\psi }{\triangle x^{2}}}+{\frac {\triangle ^{2}\psi }{\triangle y^{2}}}\\=&{\frac {\psi (x+h,y)+\psi (x-h,y)-2\psi (x,y)}{h^{2}}}\\&+{\frac {\psi (x,y+h)+\psi (x,y-h)-2\psi (x,y)}{h^{2}}}{\stackrel {\displaystyle !}{=}}0\\\rightarrow \psi (x,y)=&{\frac {\psi (x+h,y)+\psi (x-h,y)+\psi (x,y+h)+\psi (x,y-h)}{4}}\end{aligned}} $

Die Differenzen wurden mit $ \triangle $ geschrieben um eine Verwechselung mit dem Laplace-Operator zu vermeiden. Die Formel gestattet eine einfache Lösung der Laplace-Gleichung^[9]: In das Strömungsgebiet wird ein Netz mit quadratischen Maschen mit Kantenlänge h gelegt. Der Wert der Stromfunktion am Knoten mit Koordinaten (x, y) ist dann der Mittelwert der in x- und y-Richtung benachbarten Knotenwerte. Bei einem durchflossenen Kanal wird auf einem Rand die Stromfunktion zu null gesetzt und auf dem gegenüberliegenden Rand derjenige Wert festgelegt, der dem verlangten Volumenstrom entspricht. Für die Knotenwerte im Strömungsgebiet werden zunächst geschätzte Werte eingesetzt und dann iterativ mittels obiger Gleichung angepasst, bis eine zufriedenstellende Genauigkeit erreicht ist.

Zeichnerische Ermittlung von Potentialströmungen

In sechs Schritten manuell erstellte Zeichnung einer Potentialströmung um eine offene Hubschütze mittels Xfig

Potentialströmungen können auch von Hand skizziert werden, was in der Geotechnik und Hydromechanik angewendet wird^[9]. Die oben aufgeführten Eigenschaften von ebenen Potentialströmungen geben dazu Anhaltspunkte:

• Undurchlässige Ränder oder freie Oberflächen sind Stromlinien,
• Stromlinien dürfen sich nicht schneiden,
• Potentiallinien dürfen sich nicht schneiden,
• Potentiallinien und Stromlinien schneiden sich rechtwinklig und
• das Netz aus Potential- und Stromlinien kann so gestaltet werden, dass es aus annähernd quadratischen Maschen besteht.

Zu Anfang werden die Ränder des Strömungsgebiets gezeichnet (Schritt 1 im Bild) und die Richtung der Strömung am Ein- und Auslass festgelegt (2). Dann werden (3) zwischen den Rändern des Strömungsgebiets einige wenige parallele Stromlinien mit gleichen Abständen gelegt unter Beachtung der Tatsache, dass die Ränder ebenfalls Stromlinien sind. Die Potentiallinien werden so eingezeichnet (4), dass sie diese Stromlinien im rechten Winkel kreuzen und quadratische Maschen entstehen. Durch Eintragung weiterer Strom- und Potentiallinien (5,6) wird das Netz bis zum gewünschten Maß verdichtet.

Konstruktion von Geschwindigkeitspotentialen

Weil die Laplace-Gleichung linear ist, ist die Strömung, die sich aus der Summe zweier Geschwindigkeitspotentiale ergibt, wieder eine Potentialströmung. So lassen sich komplexe Strömungen durch Superposition aus einfachen Strömungen zusammensetzen, von denen einige – siehe die unten stehenden Bilder – angegeben seien:

1. Eine Parallelströmung mit konstanter komplexer Geschwindigkeit $ w=v_{x}-\mathrm {i} \,v_{y} $ ergibt sich aus $ f(z)=wz $.
2. Eine Staupunktströmung mit Staupunkt im Ursprung ergibt sich mit $ f(z)=z^{n}\,,\;n=2,3,4,\dots $
3. Eine Multipolströmung im Ursprung hat das Potential $ f(z)=z^{-n}\,,\;n=1,2,3,4,\dots $
4. Quellen haben ein Potential der Form $ f(z)={\frac {Q}{2\pi }}\ln(z-z_{0}) $. Der Ort der Quelle ist $ z_{0} $, ihre Stärke ist Q und ln ist der Natürliche Logarithmus. An der Stelle $ z=z_{0} $ befindet sich eine Singularität, in der die Laplace-Gleichung verletzt wird. Senken sind Quellen mit negativer Stärke.
5. Der Potentialwirbel – siehe unten – ergibt sich durch Vertauschung der Real- und Imaginärteile bei einer Quellströmung, was durch Multiplikation des Potentials mit -i geschieht: $ f(z)=-\mathrm {i} \,{\frac {\Gamma }{2\pi }}\ln(z-z_{0}) $.
6. Strudel ergeben sich aus der Überlagerung von Quellen/Senken und Potentialwirbel: $ f(z)={\frac {Q-\mathrm {i} \,\Gamma }{2\pi }}\ln(z-z_{0}) $.

• 

  Parallelströmung

• 

  Staupunktströmung

• 

  Multipolströmung

• 

  Quelle/Senke

• 

  Wirbel

• 

  Strudel

In den obigen Bildern sind die Höhenlinien des reellen Potentials rot und die der Stromfunktion blau gezeichnet. Der Abstand der roten Linien gibt einen Eindruck von der Strömungsgeschwindigkeit, wobei in Bereichen mit geringen Abständen die Geschwindigkeit hoch ist. Die blauen Linien sind Stromlinien. Die Funktionen, deren Höhenlinien bei den Quellen/Senken, Wirbeln oder Strudeln radial verlaufen, machen irgendwo einen Sprung, was eine Folge der Nicht-Differenzierbarkeit der Logarithmusfunktion ist.

Mit der Methode der Bildladungen kann durch geschicktes Einbringen von gedachten Quellen und Senken außerhalb des durchströmten Gebiets die Strömung so umgelenkt werden, dass sie vorgegebene Randbedingungen erfüllt.

Mit konformen Abbildungen können Strömungsfelder um einfache Grundkörper auf komplizierte Geometrien übertragen werden. Die Übertragung geschieht mit einer zweiten, komplexen Funktion w gemäß $ \Pi (z)=w(f(z)) $, die nach dem Riemannschen Abbildungssatz konform ist. Die Kutta-Schukowski-Transformation überträgt die Umströmung eines Kreiszylinders auf ein Flügelprofil, siehe das Beispiel unten. Mit der Schwarz-Christoffel-Transformation kann die Parallelströmung in der oberen Halbebene auf beliebige, mit geraden Linien berandete, einfach zusammenhängende Gebiete (und auch das innere von Polygonen) übertragen werden.

Kraftwirkungen auf umströmte Körper

Das d’Alembert’sche Paradoxon besagt, dass auf einen beliebig geformten Körper keine Kraft in Richtung der Strömung wirkt. In einem komplex differenzierbaren Geschwindigkeitsfeld übt die Strömung auch keine Kraft senkrecht zur Strömungsrichtung auf von ihr umströmte Körper aus, was eine Folgerung aus dem Integralsatz von Cauchy ist. Wenn das Geschwindigkeitspotential irgendwo innerhalb der Kontur eines Körpers nicht komplex differenzierbar ist, dann kann die Zirkulation der Geschwindigkeit längs der Kontur ungleich null sein und der Körper erfährt nach dem Satz von Kutta-Joukowski eine zu dieser Zirkulation proportionale Auftriebskraft. Mit der 1902 entdeckten Formel konnten erste auftriebserzeugende Flügelprofile entwickelt werden.

Eine bei der Berechnung der Kraftwirkung auf umströmte Körper wichtige Größe ist die Zirkulation Γ der Geschwindigkeit längs eines Weges W, die mit einem Kurvenintegral berechnet wird:

$ \Gamma :=\oint _{W}(v_{x}\mathrm {d} x+v_{y}\,\mathrm {d} y) $

Wenn die Kurve eine umströmte Kontur ist, dann kann die Zirkulation mit der komplexen Geschwindigkeit berechnet werden:

$ \Gamma =\oint _{W}w(z)\,\mathrm {d} z\quad (\in \mathbb {R} ) $

Der Integralsatz von Cauchy besagt, dass das Kurvenintegral einer komplexen Funktion zwischen zwei Punkten wegunabhängig ist, wenn die Funktion holomorph also komplex differenzierbar ist. Das Kurvenintegral verschwindet demnach entlang einer geschlossenen Kontur, wenn die Funktion in dem von der Kontur umschlossenen Gebiet holomorph ist. Die Zirkulation kann nur dann von null verschieden sein, wenn das Geschwindigkeitsfeld irgendwo innerhalb der Kontur nicht komplex differenzierbar ist^[10].

Die komplexe Kraft $ F=F_{x}-\mathrm {i} F_{y} $ (wobei $ F_{y} $ in positiver y-Richtung wirkt), die auf einen von einer ebenen Potentialströmung umströmten Körper wirkt, dessen konstanter Querschnitt die ebene Kontur W ist und dessen Ausdehnung senkrecht zum Querschnitt gleich L ist, berechnet sich mit der ersten Blasius’schen Formel

$ F=\mathrm {i} L{\frac {\rho }{2}}\oint _{W}w^{2}(z)\,\mathrm {d} z $

mit dem Kurvenintegral des Geschwindigkeitsquadrats entlang der Kontur. Der Satz von Kutta-Joukowski besagt, dass die Kraft, die auf den umströmten Körper wirkt, proportional zu seiner Zirkulation ist:

$ F=\mathrm {i} L\rho \Gamma w_{\infty }=L\rho \Gamma e^{\mathrm {i} {\frac {\pi }{2}}}w_{\infty } $

Weil die Kraft immer senkrecht zur Strömungsgeschwindigkeit $ w_{\infty } $ im Unendlichen ist, wird die Kraft auch Auftriebskraft genannt. In wirbelfreien Strömungen verschwindet die Zirkulation, so dass eine wirbelfreie Potentialströmung keine Kraft auf von ihr umströmte Körper ausübt.

Potentialwirbel

Der Potentialwirbel oder „freie Wirbel“ ist eine echte (rotationsfreie) Potentialströmung, die dennoch kreist, d. h. in einem topologisch zweifach zusammenhängenden Gebiet (wie beispielsweise dem Luftraum in einem Saal mit Mittelsäule) eine Zirkulation aufweist. Ein besonderer Potentialwirbel ist an einer freien Wasseroberfläche zu beobachten, wenn der Druck im Zentrum so gering wird, dass sich die Oberfläche merklich einsenkt und einen Wirbeltrichter ( Strudel) bildet. Reicht der Trichter unbegrenzt weit in die Tiefe, so herrscht im ganzen Flüssigkeitsgebiet Potentialströmung, nicht jedoch im luftgefüllten Kern.

Beim freien Wirbel bewegen sich alle Fluidpartikel auf konzentrischen Kreisbahnen mit Geschwindigkeits­beträgen $ v(r) $, die (außer im Kerngebiet) dem Abstandsgesetz mit Konstante $ c $ und Achsenabstand $ r $ entsprechen:

$ v(r)={\frac {c}{r}} $

Es handelt sich um eine reziproke Proportionalität, d. h. je weiter entfernt von der Achse die Partikel sind, desto langsamer bewegen sie sich, und die innersten Partikel bewegen sich am schnellsten. Dadurch ist eine völlig andere Geschwindigkeits- und Druckverteilung gegeben als beim quasi-starren Wirbel, der kein Potential besitzt und dessen Geschwindigkeit proportional zum Achsenabstand ist: $ v=\omega \cdot r. $

In realen Fluiden bilden sich freie Wirbel nur näherungsweise als Potentialströmungen aus, da in ihrer Mitte Zähigkeitskräfte zu einer quasi-starren Rotation führen und das Geschwindigkeitsfeld hier Vortizität besitzt.

Nach Bestehorn ist der Potentialwirbel eigentlich ein Punktwirbel^[11]: Das komplexe Potential des Wirbels lautet mit $ z-z_{0}=re^{\mathrm {i} \,\varphi } $ wie oben angedeutet:

$ f(z)=-\mathrm {i} \,{\frac {\Gamma }{2\pi }}\ln(z-z_{0})=-\mathrm {i} \,{\frac {\Gamma }{2\pi }}\ln \left(re^{\mathrm {i} \,\varphi }\right)={\frac {\Gamma }{2\pi }}\varphi -\mathrm {i} \,{\frac {\Gamma }{2\pi }}\ln(r) $

Auf der negativen reellen Achse bei $ \varphi =\pm n\pi \,,\;n=1,3,5,\ldots $ ist der komplexe Natürliche Logarithmus nicht differenzierbar, weswegen das Potential gar keines ist. Wohl benutzbar ist aber die Stromfunktion $ \psi =-{\frac {\Gamma }{2\pi }}\ln(r) $, die den Wirbel vollständig beschreibt. Die Wirbelstärke ist

$ \omega =-{\frac {1}{2}}\Delta \psi ={\frac {1}{2}}\Gamma \delta (z-z_{0}) $

mit dem Dirac-Delta „δ“, weshalb es sich beim Potentialwirbel um einen unendlich starken Punktwirbel an der Stelle $ z=z_{0} $ handelt, siehe Hamel-Oseenscher-Wirbel.

Beispiel

Ebene Potentialströmung um einen Zylinder und ein Flügelprofil

Das komplexe Geschwindigkeitspotential

$ {\begin{aligned}f(z)=&z+{\frac {1}{z}}=x+\mathrm {i} \,y+{\frac {1}{x+\mathrm {i} \,y}}\\=&\underbrace {x+{\frac {x}{x^{2}+y^{2}}}} _{=\phi }+\mathrm {i} \underbrace {\left(y-{\frac {y}{x^{2}+y^{2}}}\right)} _{=\psi }\end{aligned}} $

beschreibt die Umströmung eines Zylinders, denn dessen Umfang bei $ x^{2}+y^{2}=1 $ ist eine Stromlinie mit ψ=0, siehe den oberen Bildteil. Die Stromlinien sind Höhenlinien der Stromfunktion ψ und haben die Gleichung

$ y-{\frac {y}{x^{2}+y^{2}}}=\psi \quad \Rightarrow \quad x=\pm {\sqrt {{\frac {y}{y-\psi }}-y^{2}}} $

und sind im Bild im Abstand von Δψ=0,3 weiß gezeichnet. Die Stromlinie mit ψ=0 ist rot gezeichnet. Die Geschwindigkeit ergibt sich durch Ableitung des Geschwindigkeitspotentials:

$ {\begin{aligned}v_{x}-\mathrm {i} \,v_{y}=&{\frac {\mathrm {d} f}{\mathrm {d} z}}=1-{\frac {1}{z^{2}}}\\\Rightarrow \quad v^{2}=&1+{\frac {2(y^{2}-x^{2})+1}{(x^{2}+y^{2})^{2}}}\end{aligned}} $

In Abwesenheit eines Schwerefeldes liefert die Bernoulli-Gleichung den Druck:

$ {\frac {\rho }{2}}v^{2}+p=E\quad \Rightarrow \quad p=E-{\frac {\rho }{2}}\left(1+{\frac {2(y^{2}-x^{2})+1}{(x^{2}+y^{2})^{2}}}\right) $

Mit der konformen Abbildung

$ w(z)=z+z_{0}+{\frac {R^{2}}{z+z_{0}}}\quad {\text{mit}}\quad R=\Re (z_{0})+{\sqrt {1-\Im (z_{0})^{2}}} $

wird der Zylinder auf eine Kontur transformiert, die einem Flügelprofil ähnelt^[12], siehe den unteren Bildteil, wo $ z_{0}=0{,}15\,e^{\mathrm {i} {\frac {5}{6}}\pi } $ und $ R=0{,}8672 $ ist. Die Funktionen $ \Re $ und $ \Im $ extrahieren den Real- bzw. Imaginärteil ihres komplexen Arguments. Der Betrag von $ z_{0} $ kontrolliert die Bauchigkeit, wohingegen die Phase die Wölbung des Profils beeinflusst.

Die Strömung wird wie die Kontur transformiert, so dass sich die Stromlinien in der w-Ebene mit

$ w(z)=z+z_{0}+{\frac {R^{2}}{z+z_{0}}}\quad {\text{und}}\quad z=\pm {\sqrt {{\frac {y}{y-\psi }}-y^{2}}}+\mathrm {i} \,y $

ergeben. Sie sind im unteren Bildteil weiß gezeichnet. Die Stromlinien dieses Profils wurden oben, im Abschnitt #Analogon der Wärmeleitung, mit den Ergebnissen aus einer Wärmeleitungsanalyse verglichen.

Weblinks

• K. Lüders, R. O. Pohl, G. Beuermann, K. Samwer: Stromlinien-Modellversuche. IWF Wissen und Medien, 2004, abgerufen am 3. Januar 2021. 

Einzelnachweise

Literatur

• J. H. Spurk: Strömungslehre. Einführung in die Theorie der Strömungen. 8. überarbeitete Auflage. Springer Verlag, Heidelberg, Dordrecht, London, New York 2010, ISBN 978-3-642-13142-4, S. 343 ff., doi:10.1007/978-3-642-13143-1 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 2. Januar 2021]). 
• Michael Bestehorn: Hydrodynamik und Strukturbildung. Springer, Berlin u. a. 2006, ISBN 3-540-33796-2. 
• Ralf Greve: Kontinuumsmechanik. Ein Grundkurs für Ingenieure und Physiker. Springer, Berlin u. a. 2003, ISBN 3-540-00760-1. 
• Hans J. Lugt: Wirbelströmung in Natur und Technik. G. Braun, Karlsruhe 1979, ISBN 3-7650-2028-1. 
• Herbert Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 11., überarbeitete und erweiterte Auflage. Vieweg, Braunschweig u. a. 2002, ISBN 3-528-48209-5. 
• Heinz Schade, Ewald Kunz: Strömungslehre. 2., durchgesehene und verbesserte Auflage. de Gruyter, Berlin u. a. 1989, ISBN 3-11-011873-4. 
• Jürgen Zierep: Grundzüge der Strömungslehre. 4., überarbeitete Auflage. G. Braun, Karlsruhe 1990, ISBN 3-7650-2039-7.